BreakEven

How to Calculate Break-Even Analysis in Excel: A Step-by-Step Guide

by accountingfinancial analysis

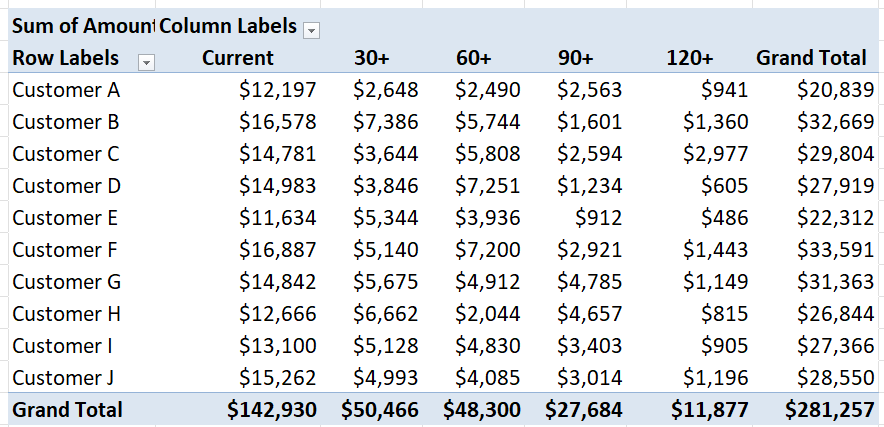
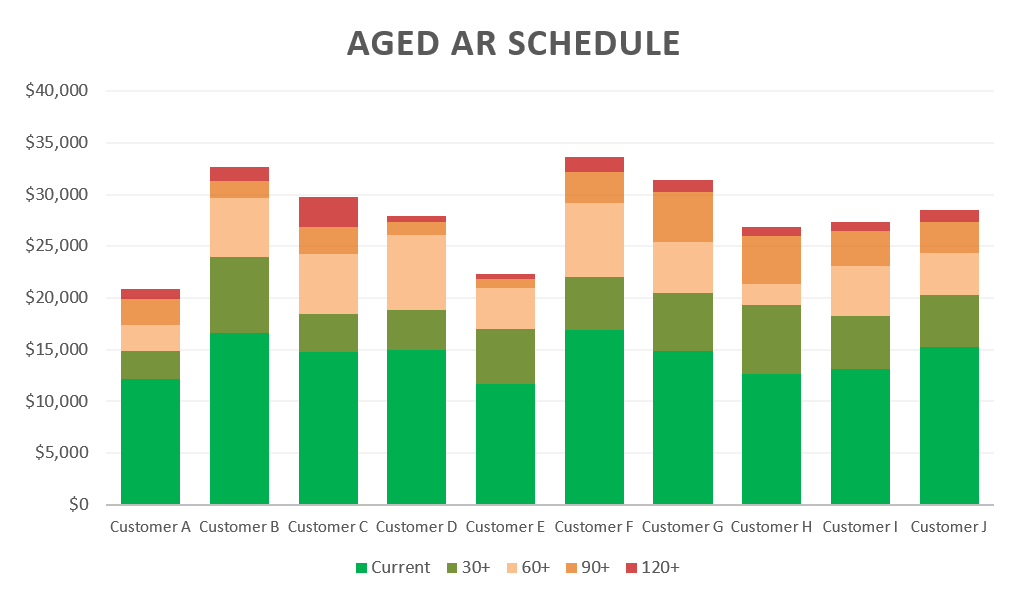
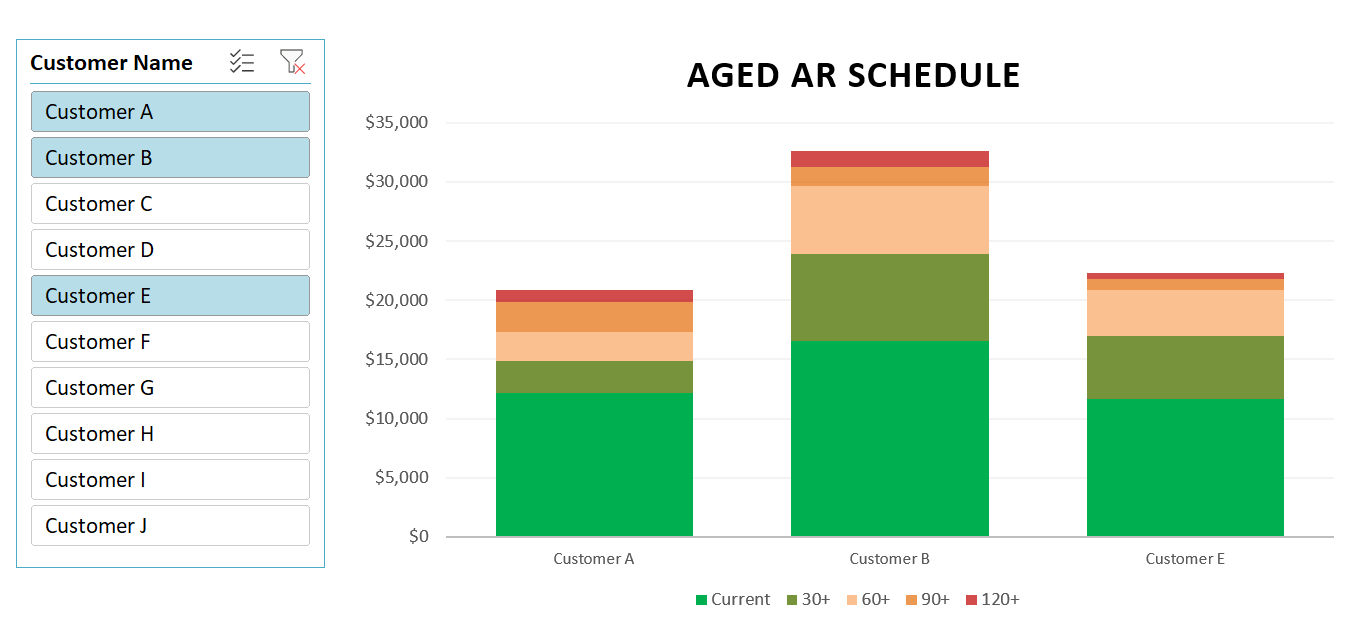
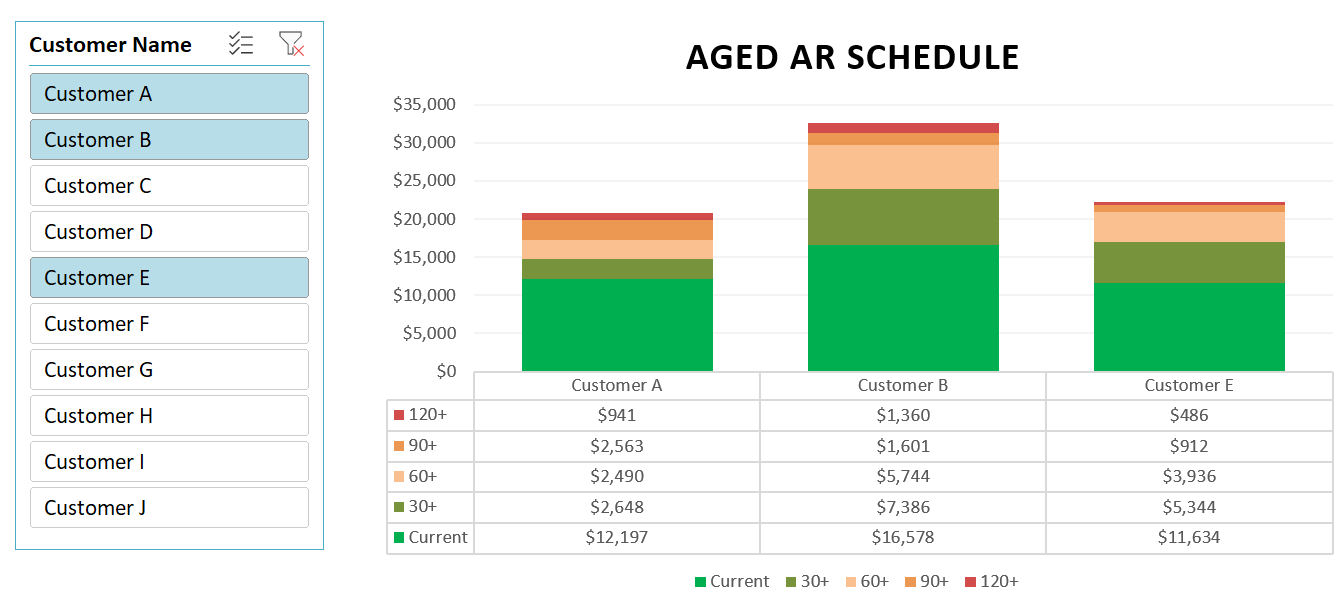
Every business owner, financial analyst, and student asks the same fundamental question: “How much do I need to sell to cover my costs?”

This is what your break-even point would be. It is where your total revenue equals your total costs, yielding zero profit, but also zero loss. This is a crucial number because you know if you produce more than what’s needed to hit break even, you’ll be turning a profit. Calculating this manually can be time-consuming, but building a dynamic break-even analysis in Excel can enable you to test different pricing strategies and cost structures instantly. In this guide, I’ll walk you through the process, the formulas, and how to visualize the data using Excel charts.

What is a Break-Even Analysis?

Before opening Excel, it is crucial to understand the three components that make up the break-even calculation:

  1. Fixed Costs: Expenses that stay the same regardless of how much you sell (e.g., rent, insurance, salaries).
  2. Variable Costs: Expenses that increase with every unit sold (e.g., raw materials, shipping, packaging).
  3. Selling Price: The amount you charge for one unit of your product.

The formula to find the number of units you need to sell to break even is:

Break-Even Units = Fixed Costs/(Selling Price - Variable Cost per Unit)

The denominator (Selling Price – Variable Cost) is also called the Contribution Margin. It represents how much money is left over from each sale to contribute toward paying off your fixed costs. If your contribution margin is not positive, then you’ll never been able to hit your break-even point.

Now that we understand the terms and key formulas, we can move on to setting up the break-even calculation in Excel.

Step 1: Set Up Your Data Table

First, we need to input our variables. Open a new Excel sheet and create a distinct input area. This makes it easy to change numbers later without breaking your formulas.

Let’s pretend we are running a specialized T-shirt business, with the following costs and selling prices:

A table showing fixed costs, variable costs, and selling price per unit in Excel.

Step 2: Calculate the Break-Even Point

Now, let’s calculate the exact number of T-shirts we need to sell to cover that $5,000 in fixed costs. Using the aforementioned formula where we take the fixed costs and divide them by the contribution margin (selling price less variable cost), this results in the following calculation:

A sample break-even calculation in Excel.

The formula in cell C6 is as follows:

=ROUNDUP(C2/(C4-C3),0)

The result is 333.33 units, but that ROUNDUP function rounds the result up to the nearest whole number, which is 334. Since you can’t sell a portion of a shirt, it’s necessary to round up.

Step 3: Create a Dynamic Data Model

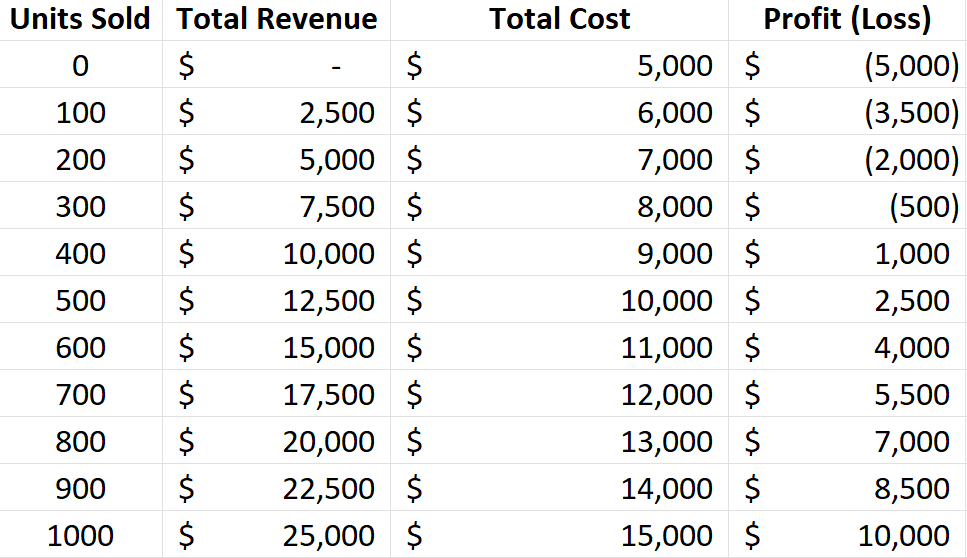
Knowing the break-even point is helpful, but seeing the trend can be much more useful. Let’s create a table that calculates revenue and costs at different volume levels (e.g., selling 0 units, 100 units, 200 units, etc.).

I’m going to set up a table with headers for the following fields: Units Sold, Total Revenue, Total Cost, and Profit (Loss). For Units Sold, the units will start from 0 and increment by 100 at a time. The Total Revenue field will multiply the units sold by the selling price. The Total Cost field will be equal to the units sold multiplied by the variable cost, with the fixed costs added on top. The Profit (Loss) will take the Total Revenue and deduct the Total Cost.

The table should look something like this:

Break-even table in Excel showing cost and revenue.

Step 4: Visualize with a Break-Even Chart

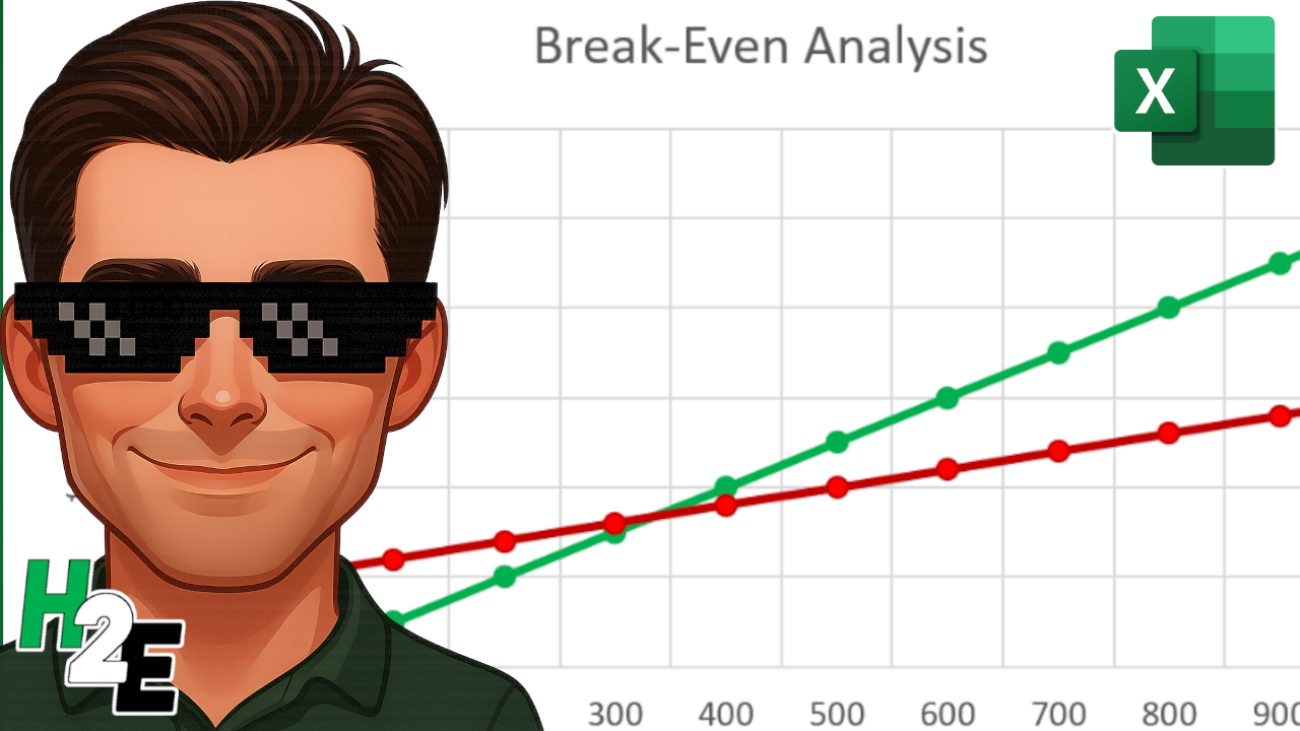
Visuals make financial data easier to understand. We can create a chart that shows where the Total Revenue line crosses the Total Costs line.

To do this, start by highlighting three columns in your data table: Units Sold, Total Revenue, and Total Costs. Go to the Insert tab, open up the Charts window, and select any Line Chart you wish to use. You’ll need to adjust the data so that the Horizontal Axis Label for the Revenue and Cost fields is the Units Sold column.

    You should now see a chart that looks similar to this:

    A chart showing break-even analysis in Excel.

    As per the earlier analysis, we can see that the break-even point is right around 300 units, which is what the chart above indicates.

    Step 5: Advanced Tip: Use Goal Seek to do a What-If Analysis

    What if you don’t just want to break even? What if you want to make exactly $2,000 in profit this month? You can use Excel’s Goal Seek feature rather than guessing. In the following example, I’ve setup a couple of extra cells for units sold and one for profit (loss), which will be used in the goal seek calculation:

    Break-even calculation in Excel that shows units sold and profit (loss).,

    Now, let’s go to the Data tab, select What-If Analysis (under the Forecast section), and click on Goal Seek.

    Selecting goal seek from the what-if analysis.

    Based on the table above, let’s input the following values for the Goal Seek inputs:

    Setting up the goal seek function in Excel to calculate units needed for a specific profit.

    The Set cell value is the ending value that we want, which in this case is the Profit (Loss) value, which is determined by selling price, variable cost, and fixed costs. We want this value to equal 2000, by changing cell C8, which is the number of units sold. After clicking OK, Goal Seeks does the work to figure out what the value in C8 needs to be for C9 to be equal to 2000.

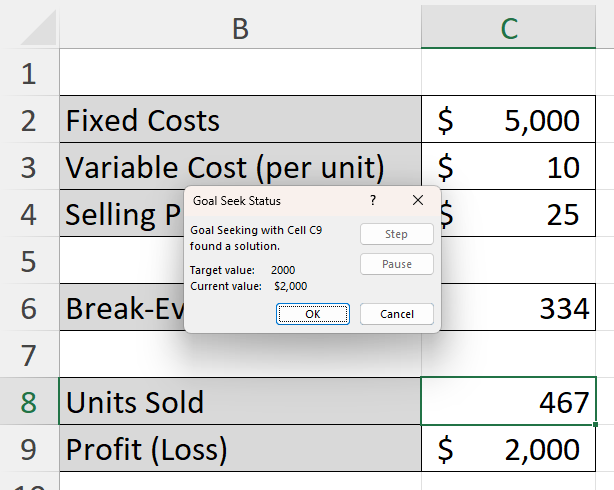
    Results of a goal seek calculation in Excel.

    By clicking on OK, you’ll accept the results and they’ll remain in your table. This calculation tells me that by selling approximately 467 units, the profit will be $2,000.

      If you liked this post on How to Calculate Break-Even Analysis in Excel: A Step-by-Step Guide, please give this site a like on Facebook and also be sure to check out some of the many templates that we have available for download. You can also follow me on X and YouTube. Also, please consider buying me a coffee if you find my website helpful and would like to support it.

      Sales data set in Excel.

      How to Do an 80/20 Sales Analysis in Excel

      by accountinganalysis

      Marketers know that typically 80% of sales come from just 20% of customers, and by focusing on that group, you can gain valuable insights into your data. With the help of Excel, it’s easy to determine not only who your top 80% of customers are, but also how much revenue they’re actually bringing in. In the example below, we’re going to go over how to do such an analysis, and identify how much your top 20% and bottom 20% of customers generate.

      And you can also do further analysis by looking at the top 10% or whatever cutoff points you want. In this example, we’ll create a spreadsheet which will allow you to set these different cutoff points however you want.

      This is the data set that I’m going to use for this example.

      Sales data set in Excel.

      Step 1: Convert the data into a pivot table

      The first thing we’ll want to do is to convert this into a pivot table. By doing this, we can sum up the totals by individual customers. We don’t want to apply the analysis on raw numbers as that will only give us the top invoices when instead, we’re looking at sales by customers.

      If you select a cell on the data and go to the Insert tab, you can click on the button to create a Pivot Table. Then, pull the sales data into the fields section and the customer field into the Rows section. This now creates a summary by customer.

      Pivot table showing sales by customer.

      Step 2: Calculate the cutoff points

      Now that the data is grouped by customer, we can start to calculate the sales by different percentiles. If you want to determine the top 20%, then we need to get the 80% percentile. At that level, the values will be higher than 80% of the rest of the data, and thus, leave us with the cutoff for the remainder, the top 20%.

      With the sales data in column B, we can use the following formula to get this cutoff point:

      =PERCENTILE(B:B,0.8)

      The 0.8 indicates the 80% percentile, which means that the value returned is higher than 80% of the values in the data set. In my data set, this returns a value of 276.34. Any customer whose total is at or above this cutoff point means that they are part of the top 20%.

      To get the cutoff value for the bottom 20%, the same formula is used, except now for the second argument, the value is set to 0.2. This returns a value of 101.90. In this situation, we’ll be focusing on values at or below this cutoff.

      Step 3: Calculate the sales that fall within the top and bottom 20%

      Now, let’s calculate the total dollar amount of the sales that fall in the top and bottom 20% ranges. For the top 20%, we’ll need to sum up all the values that are equal to or greater than that cutoff point of 276.34. With that value in cell B3, my formula is as follows:

      =SUMIF($B$9:$B$1000,”>=”&$B3)

      The pivot table sales field is in column B. This calculation returns a value of $35,072. That is the total dollars that my top 20% of customers have generated.

      To calculate the bottom 20%, we can use the following formula, assuming that the cutoff point for 101.90 is in cell B4:

      =SUMIF($B$9:$B$1000,”<=”&$B4)

      The total of this value is 7,894, and that indicates how much revenue the bottom 20% have brought in.

      We can visualize these data points by plotting them on a column chart:

      If you want to calculate different percentiles and cutoff points, you just need to adjust the second argument in the percentile formula.

      If you liked this post on How to Do an 80/20 Sales Analysis in Excel, please give this site a like on Facebook and also be sure to check out some of the many templates that we have available for download. You can also follow me on Twitter and YouTube. Also, please consider buying me a coffee if you find my website helpful and would like to support it.

      AgedARReport1

      Create an Accounts Receivable Aging Report in Excel

      by accountingaccounts receivable

      An aged accounts receivable (AR) report can help you identify accounts with overdue receivables. It can help you stay on top of your AR to ensure that you are prioritizing collection efforts based on their relative ages.

      Here’s a sample of what your AR data might look like, showing customers, invoice dates, due dates, and amounts:

      Using a pivot table, we can summarize these details to determine how old the AR is, and create a report to help us stay on top of overdue accounts.

      Creating the accounts receivable table

      First, I’ll convert this data into a table, and call it tblAR. By creating a table, it will make it easy to add to the data and update it, and for the pivot table to refresh easily as new data is entered. Next, I’ll add a column to calculate the number of days past due. The formula for that is as follows:

      =IF([@[Due Date]]>TODAY(),0,TODAY()-[@[Due Date]])

      Now my table shows the number of days past due. And since it uses the TODAY() function, it will automatically update.

      A table containing accounts receivable data.

      Next, I need to create a lookup table for the aging, which I’ve setup as follows:

      Then, I’ll create a lookup formula to determine what the description should be based on how old the receivable is. In my spreadsheet, the lookup table is in columns H and I. The following formula will pull in the ‘description’ field:

      =VLOOKUP([@[Days Past Due]],H:I,2,TRUE)

      Now I have a complete table that shows the correct aging category based on the days past due:

      Setting up the pivot table

      Once the data is ready to go, the next step is to create the pivot table. When putting the Aging Category in the Rows section and the Amount in the Values section, this is what the pivot table looks like:

      A pivot table summarizing invoices by age.

      This gives me a broad high-level overview of the overall aging. However, I can also set this up so that it breaks it down by customer. For that setup, I can put the Customer Name field in the Rows section, and the Aging Category going across in columns:

      A pivot table breaking down aged receivables by customer.

      I have dragged the ‘Current’ value to the front to ensure that the text value is at the start. Next, I will create a chart to help visually show the aged AR data. Since there are multiple aging categories per customer, a stacked column chart is ideal in this situation. Then, after applying custom formatting colors to each aging category, I have a visual representation of the AR aging chart:

      An aged accounts receivable report displayed using an Excel chart.

      If you have a lot of customers and can’t fit all of them on a single chart, you could insert a slicer to make it easy to select one or multiple customers.

      An aged accounts receivable report displayed using an Excel chart and slicers.

      To help visualize this further, I can also add a data table that shows the breakdown of the different aging categories. To enable this, select the chart, click on the Design tab, select Add Chart Element and select a Data Table With Legend Keys:

      An aged accounts receivable report displayed using an Excel chart and slicers and a data table.

      If you like this post on How to Create an Accounts Receivable Aging Report in Excel please give this site a like on Facebook and also be sure to check out some of the many templates that we have available for download. You can also follow me on Twitter and YouTube. Also, please consider buying me a coffee if you find my website helpful and would like to support it.

      Amortization calculator which calculates values for a specific period.

      Create an Amortization Calculator in Excel

      by accountingamortizationcalculatorfunctions

      Amortization schedules are essential tools for anyone managing a loan or mortgage, providing a clear breakdown of how payments are allocated towards interest and principal over the loan’s term. Typically, these schedules detail each payment’s date, the interest portion, the principal portion, and the remaining balance, offering borrowers insight into the precise cost of borrowing over time.

      Creating an amortization schedule in Excel can be a time-consuming process, but with the help of some advanced payment functions, you can expedite the process and even eliminate the need for creating an entire amortization table.

      Generating the key components of an amortization schedule

      Whether you’re creating a full-blown amortization schedule or just want to calculate the balance at a future point in time, you’ll need to know the following values before you can begin:

      • the loan value,
      • the interest rate and compounding,
      • the number of periods, and
      • the start date of the loan

      Suppose you have a $500,000 loan with a 5% interest rate, which is for a period of 10 years, and that payments are made on a monthly basis. Given this information, you can start by calculating the monthly payment amount. Here’s what the inputs would look like for the PMT function:

      =PMT(0.05/12,10*12,-500000,0) = 5,303.28

      This assumes compounding to be monthly, hence the need to divide the interest rate by 12. And the negative 500,000 balance tells the function that this is an amount owing and that it will reduce over time. The following argument, 0, is to signify that the future value is 0.

      There is also an additional argument, for whether the payments are made at the beginning or the end of the period. The default is set to the end of the period. If payments are made at the beginning, then the final argument is set to 1. If the payment is at the start, then the payment value would change to $5,281.27, assuming all the other values remain the same. But for the purposes of these examples, we’ll assume payments are made at the end of the period.

      Creating a calculator for specific month’s calculations

      Now that you have all the necessary variables, including the payment amount, you can start to create the calculator.

      In this first case, we’ll look at how to calculate values for just a specific period. Let’s assume the loan’s start date is January 1, 2024. And let’s assume we want to calculate what the balance, interest, and principal payment amount will be for the month of Dec 2025.

      How to calculate amortization amounts for a specific period:

      1. Start with calculating the period number. One function that can help with this is the DATEDIF function. By using it, you can quickly calculate the difference between two time periods. Here’s how it would work in this example:

      =DATEDIF(“1/1/2024″,”12/1/2025″,”m”) = 23

      Two full years have not fully elapsed until we get to 1/1/2026. But since we want to calculate the values for the 24th month, we’ll need to add 1 to the equation. The formula to calculate the current period will be as follows:

      =DATEDIF(“1/1/2024″,”12/1/2025″,”m”)+1

      2. Calculate the interest payment for the period. To get the interest amount, use the IPMT function:

      =IPMT(0.05/12,24,120,-500000) = 1,760.19

      3. Calculate the principal amount paid down during the period. In this case, we can use the PPMT function. It is the same setup as the previous formula:

      =PPMT(0.05/12,24,120,-500000) = 3,543.08

      4. Calculate the ending value as of that period. Using the FV function, here’s the formula to get the ending balance as of the end of Dec 2025:

      =FV(0.05/12,24,5303.28,-500000) = 418,902.68

      By using these functions, you no longer need to make an entire amortization schedule. You can simply do a calculation for the period you need to sum up the values for. By creating inputs for the start of the loan, loan amount, interest rate, # of periods, and the period you want to calculate for, you can setup an amortization calculator as follows in Excel:

      Amortization calculator which calculates values for a specific period.

      Calculate amortization values for a specific range

      Suppose you wanted to calculate the interest and payment values for all the months in 2025. This can be a bit trickier since we aren’t calculating amounts for just a single period anymore. Instead, we need to get a range of values.

      How to calculate amortization amounts for a specific multiple periods:

      Step 1. Get the correct period numbers. Let’s assume the loan began on June 1, 2023. We need to get the starting period number, which is Jan. 1, 2025. This can be done with the DATEDIF function:

      =DATEDIF(“6/1/2023″,”1/1/2025″,”m”)+1 = 20

      This tells us that January is the 20th month of the loan. If January is the 20th month, then that also means if we add 11, that December will be the 31st month of the loan. Thus, our range of periods is 20 through 31. You could, however, use the DATEDIF function to do the calculation for that period as well.

      Step 2. Calculate the interest payments for the year. Now that we know the periods we need to calculate the interest for, we can use the CUMIPMT function:

      =-CUMIPMT(0.05/12,120,500000,20,31,0) = 20,851.88

      The present value cannot be set to negative for the cumulative function, or else you will get an error. To adjust for this and avoid a negative value, simply add a dash before the function to ensure the result is flipped from a negative value to a positive one.

      Step 3: Calculate the total of the principal payments made during the period. To calculate the principal paid during the period, we can use the CUMPRINC function. The inputs are the same as that of the cumulative interest payment calculation:

      =-CUMPRINC(0.05/12,120,500000,20,31,0) = 42,787.43

      Step 4. Get the ending period’s balance. Just as with the previous section, we can use the same FV calculation to get the ending balance. This time, it will be for period 31.

      =FV(0.05/12,31,5303.28,-500000) = 393,684.23

      Here is how the calculator could be setup to make these calculations based on a range.

      Amortization calculator which calculates values for a specific range.

      You can download the amortization calculator I have created from these examples here.

      If you liked this post on How to Create an Amortization Calculator in Excel, please give this site a like on Facebook and also be sure to check out some of the many templates that we have available for download. You can also follow us on Twitter and YouTube.

      BankRecGeneric

      Bank Reconciliation Template 2024: Use Auto-Matching Rules to Speed Up Your Recs!

      by accountingbank reconciliationtemplatevba

      Introducing the Ultimate Bank Reconciliation Excel Template – your time-saving companion for hassle-free financial management!

      Are you tired of spending hours manually matching transactions and dealing with duplicates during your bank reconciliations? Look no further! This downloadable Excel file is here to revolutionize the way you handle your finances. Packed with powerful features and user-friendly functionalities, this template will streamline your reconciliation process like never before.

      Key features

      Automated Transaction Matching: Say goodbye to tedious manual matching. This Excel template is equipped with an intelligent algorithm that automatically matches transactions, making your reconciliation process a breeze. Experience unmatched efficiency as the template swiftly identifies and pairs up corresponding transactions, freeing up your valuable time.

      Effortless Manual Matching: Whatever the template doesn’t end up matching, you can do so manually using the Reconciler. It’s a much easier process than the manual approach as once you select a transaction, it will find related transactions that you can match the transaction to. Simply review the related items displayed, and with a few clicks, you’ll have your transactions matched accurately and swiftly.

      Using the bank reconciliation template to easily match transactions.

      Duplicate Detection: This template also checks for duplicates and will be careful not to match any items where there is a duplicate entry. You can still match these transactions manually using the Reconciler, but you won’t have to worry about the template automatically matching items where there are duplicates. This helps ensure accuracy and integrity when doing the automatic matching.

      Flexible Matching Rules: Take full control of your reconciliation process with customizable matching rules. The Excel template empowers you to create rules to automatically match transactions on a 1-to-1 basis or 1-to-many, tailored to your unique needs.

      Matching rules in the bank reconciliation template.

      By creating these rules, you can specify how a transaction should be classified.

      In the above example, if a description contains CK#, then it will belong to the ‘Checks’ category. For the key, which is used to help match a transaction, it will take the next 4 numbers. So if you have CK#1234, then 1234 would be the key. For a transaction to automatically match, it will need to be part of the same category, have the the same key, and amount. In the case of 1-to-1 matches, it will only need to find another transaction that matches this criteria. The one exception is if there is a duplicate; in that case, the transactions won’t automatically match. The auto-match is designed to minimize false matches.

      For the Wire Transfer example above, it will simply use the date as the key. Since it’s a 1-to-1 match, it will look for another Wire Transfer on the same date with the same amount.

      The deposit example shown above is slightly different in that it relies on the date but it is a 1-to-Many match type. However, this can also work as a many-to-many matching type as well. That’s because it will look for all of the deposits on that date, across the book, bank, and previous outstanding items. Only if the total of all the deposits on that date are a match will the auto-match rules kick in and say that everything is a match. You might use this type of matching if you have multiple deposits on the GL side that total just a single deposit amount on the bank side, or vice versa.

      Easy Overrides. If you need to force a match, you can do so by entering any value in the ‘Manual Override’ column. This will clear the O/S status and indicates that the transaction has been matched. In the example below, just entering an ‘X’ is enough to mark off a transaction as being reconciled:

      Overriding a transaction on the bank reconciliation template.

      Quickly Generate Reports and Start a New Month: With just a click of a button, this Excel template generates a comprehensive report summarizing outstanding items. Gain valuable insights into your financial status and easily identify discrepancies that require attention. Stay on top of your bank reconciliations with accurate, up-to-date information at your fingertips. Clicking on the Reconcile Month button will summarize your outstanding items. You can also clear all the data with the Clear Data button. Click the New Month button when you’re done reconciling and want to close out the month. It will transfer all your current outstanding items to the previous outstanding items tab.

      Buttons on the bank reconciliation file.

      Try the bank reconciliation template for yourself!

      Whether you’re a small business owner, a financial professional, or an individual managing personal finances, this Bank Reconciliation template is your go-to solution. Experience unparalleled ease, accuracy, and efficiency in your reconciliation process. Save time, reduce errors, and take control of your financial management like never before.

      Best of all, you can try it out for free to see how you like it. Download the trial version here. If you decide you want to buy the full version without restrictions and full VBA code available, click on the following button:

      If you like this Bank Reconciliation template, please give this site a like on Facebook and also be sure to check out some of the many templates that we have available for download. You can also follow me on Twitter and YouTube. Also, please consider buying me a coffee if you find my website helpful and would like to support it.

      NPVIRR

      How to Calculate Net Present Value (NPV) and Internal Rate of Return (IRR) in Excel

      by accountingfinancial analysis

      What is Net Present Value (NPV)?

      Net Present Value (NPV) is a financial metric used to determine the current value of a series of cash inflows and outflows. It takes into account the time value of money, which means that a dollar received in the future is worth less than a dollar received today due to factors like inflation and the opportunity cost of not having that money available to invest in other projects.

      The calculation of NPV involves discounting the expected future cash flows of a project or investment back to their present value using a specified discount rate. The result is the difference between the present value of the expected cash inflows and outflows.

      NPV is an important calculation because it helps you evaluate the profitability and feasibility of an investment. It can also allow you to compare the expected returns of different investment opportunities, and to make informed decisions about which projects to pursue.

      If the NPV is positive, it means that the project is expected to generate more cash inflows than outflows, and thus, it’s a profitable investment opportunity. However, if the NPV is negative, the project is expected to result in a net loss and is therefore not considered a viable option.

      The NPV calculation is an important tool in finance as it can help decision makers determine whether to move forward on a project.

      What is the Internal Rate of Return (IRR)?

      The Internal Rate of Return (IRR) is used to measure the profitability of an investment project or opportunity, often in conjunction with calculating NPV. It is the discount rate where the present value of expected cash inflows equals the present value of expected cash outflows, or when NPV is equal to 0.

      IRR represents the rate of return at which an investment will break even over its lifetime. It is shown as a percentage. And if you use the IRR percentage as your discount rate in the NPV calculation, the result will be an NPV of 0.

      With Excel, you can quickly calculate the IRR through a simple formula, rather than having to go through a time-consuming process that might otherwise involve trial and error.

      Calculating NPV and IRR in Excel

      To illustrate how to calculate NPV and IRR, I’ll use the following example. Suppose that you are investing $1,000 into a project that will generate the following cost savings:

      • Year 1: $50
      • Year 2: $100
      • Year 3: $250
      • Year 4: $300
      • Year 5: $600

      In total, that is $1,300 in cost savings. Although that’s more than the original $1,000 investment, those savings are spread out over a period of five years. To get a true picture of whether the project is worthwhile, you need to adjust for the time value of money and adjust those amounts and calculate their present values — what their values are today. This is where the NPV function comes into play.

      However, before using the NPV function, you need to determine the discount rate that you are going to use. The discount rate is important as it tells you the interest rate that you will be using when adjusting the cost savings back to today, and to calculate the present value. If the discount rate is high, then it’ll be more difficult for the NPV calculation to be positive (and hence, suggest that the investment should be taken on). And if the discount rate is too low, then it could be too easy to clear the bar and for the NPV formula to suggest the project is worthwhile.

      The discount rate should be higher than the risk-free rate since you are taking on some risk, and thus, you should be compensated for doing so. If you were to use the same rate as what you could earn on a treasury bill or a bank deposit, there would be little incentive to go ahead with the project even with a positive NPV. After all, what’s the point of taking on the risk if you’re not getting a better return?

      In this example, I’m using a discount rate of 5%. This is what the NPV formula will look like with all of the inputs:

      =NPV(0.05,50,100,250,300,600)-1000

      As you can see, the order of the values is important as that will determine how many periods each value will be discounted by. The result of this formula is a value of $71.21. It’s a positive amount, indicating that the project should be undertaken as the present value of the future cost savings offset the current investment.

      To prove that calculation out, I’ll show you how this calculation could be done manually. Here, for example, is how the present value would be calculated for the $50 in cost savings that is achieved in year 1:

      =50*(1+0.05)^-1

      One plus the discount rate is raised to a power of negative one to bring the value back one period, using the discount rate. That returns a value of $47.619. Here are the other present value calculations:

      • Year 2 ($100) : $90.703
      • Year 3 ($250) : $215.959
      • Year 4 ($300) : $246.811
      • Year 5 ($600): $471.116

      If you add all of these present values up, they total $1,071.21. And that is $71.21 more than the $1,000 initial investment, which is the same result as the NPV formula.

      One thing you may be wondering is at what point does the value equal 0 — where is the breakeven? This can be calculated using the IRR formula. In Excel, this is a simple formula that just takes all the inflows and outflows. For example, if you had the negative investment amount of $1,000 in cell A1 followed by the cost savings in the the adjacent columns (until column F), then the formula for IRR would be as follows:

      =IRR(A1:F1)

      The end result is a value of 6.8576%. If you use this as the discount rate in the NPV calculation, you will get an NPV value of 0. This tells you that if you use a discount rate higher than this percentage, your NPV value will be negative as the level of discounting will be too high for the project to have a positive NPV value. On the other hand, anything below the IRR rate will result in a positive NPV value and thus indicate that the project should move forward.

      If you liked this post on How to Calculate Net Present Value and Internal Rate of Return in Excel, please give this site a like on Facebook and also be sure to check out some of the many templates that we have available for download. You can also follow me on Twitter and YouTube. Also, please consider buying me a coffee if you find my website helpful and would like to support it.

      15ExcelAccounting

      15 Excel Functions Accountants Should Know

      by accountingadvancedaverageaveragesbeginnercountcountifdatesfunctionsindexintermediatelookuplookupsmatchsumsumifsumifsuniquevlookup

      If you’re an accountant, you know that working with large amounts of data can be a daunting task. But with Excel, that work can get a whole lot easier and more efficient. Understanding Excel’s advanced features and functions can improve productivity, reduce errors, make your work more accurate, and most importantly — save you time. Below, I’ll go over some of the most important Excel functions that accountants should know, and provide examples of how to use them. For this example, I’ll use the following spreadsheet. Feel free to download it and follow along with the calculations.

      1. SUM

      The SUM function is a basic but essential function in Excel. It allows you to add up a range of values, which is helpful when calculating totals, such as revenue, expenses, and profits. Suppose you have a spreadsheet with sales data. In the above example, the total sales are in column G. If you wanted to sum up the entire column, the formula would be as follows: =SUM(G:G)

      2. AVERAGE

      The AVERAGE function calculates the average of a range of values. It is useful when analyzing data and preparing financial statements. In the above example, suppose you wanted to calculate what the average sale was. To do this, you can just use the AVERAGE function on column G, similar to the SUM function before. Here’s the formula: =AVERAGE(G:G)

      3. IF

      The IF function allows you to test a condition and return one value if the condition is true and another value if the condition is false. This can be useful because it can send your formulas to the next level. By knowing to use the IF function, you could also use SUMIF, AVERAGEIF, and many other functions that involve an if statement. In the above example, let’s say you only wanted to know if a value in cell M2 was part of the Motorcycles product line. The formula would be as follows: =IF(M2=”Motorcycles”,1,2). If it is part of Motorcycles, you would have a value of 1, otherwise, it would be 2.

      4. SUMIF

      By knowing the SUM and IF functions, you can combine them together with SUMIF, which is an incredibly popular function. It gives you a quick way to tally up the totals that meet a criteria. For example, let’s say you want all sales that relate to the Motorcycles category. The formula for that would be as follows: =SUMIF(M:M,”Motorcycles”,G:G). If the criteria is met in column M, then the formula will sum up the corresponding values in column G. There’s also the super-powered SUMIFS function, which allows you to combine multiple criteria.

      5. EOMONTH

      The EOMONTH function calculates the last day of the month for a specified number of months in the future or past. It is useful when working with data that is organized by date. For accountants, this can be useful when you’re calculating when something is due. Let’s say in this example, we need to calculate the date orders need to go out on, and that needs to be the end of the next month. Using the ORDERDATE field in column H, here’s how that calculation would look in the first cell, which would then be copied down for the rest: =EOMONTH(H2,1)

      6. TODAY

      The TODAY function is helpful for accountants in calculating deadlines and knowing how many days are remaining or past a certain date. Suppose that you wanted to know how many days have past since the ORDER DUE DATE that was calculated in the previous example. Rather than entering in a static date that every day you would need to change, you can just use the TODAY function. Here’s how a formula calculating the days since the deadline for the first cell would look like, assuming the due date is in column N: =TODAY()-N2. The next day you open up the workbook, the calculations will update to reflect the current date; there’s no need to make any changes. There are many more date calculations you can do in Excel.

      7. FV

      The FV function calculates the future value of an investment based on a fixed interest rate and a regular payment schedule. You can use it to calculate the future value of an investment or savings account. Let’s say that you wanted to save $10,000 per year and expect to earn a return of 5% per year on that investment. Using the FV calculation, you can do that with the following formula: =FV(0.05,5,-10000). If you don’t enter a negative for the payment amount, the formula will result in a negative value. You can also specify whether payments happen at the beginning of a period (1) or end (0 — this is the default) with the last argument in the function.

      8. PV

      The PV function lets you do the opposite and work backwards from a future value to the present. Knowing that the calculation in example 7 returns a value of $55,256.31, that can be used in the PV calculation to check our work: =PV(0.05,5,10000,-55256.31). The formula returns a value of 0, which is correct, as there was no starting value in the FV calculation.

      9. PMT

      The PMT function calculates the periodic payment required to pay off a loan with a fixed interest rate over a specified period. It is helpful when determining the monthly payments required to pay off a loan or mortgage. Let’s take the example of a mortgage payment where you need to pay down $500,000 over the period of 30 years, in monthly payments. At a 5% interest rate, here’s what the payment calculation would be: =PMT(0.05/12,12*30,-500000,0). Here again the ending value needs to be a negative to avoid a negative value in the result. And since the payments are monthly, the periods need to be multiplied by 12 and the interest rate is dividend by 12.

      10. VLOOKUP

      The VLOOKUP function allows you to search for a value in a table and return a corresponding value from another column in the same row. It’s one of the most common Excel functions because of how useful and easy to use it is. It is helpful when working with large data sets and performing data analysis. Let’s suppose in this example that you want to find the sales related to order number 10318. The formula for that calculation might look like this: =VLOOKUP(10318,C:G,5,FALSE). In a VLOOKUP function, you need to specify the column number you want to extract from, which is what the 5 represents. If you’re using Office 365, you can also use the newer, flashier XLOOKUP function. I put VLOOKUP on this list because it’ll work on older versions of Excel — XLOOKUP won’t.

      11. INDEX

      The INDEX function allows you to return a value from a data set by specifying the row and column number. It’s also helpful if you just want to return data from a single row or column. For example, the sales column is in column G. If I know the order number is on row 20 (which relates to order number 10318), this formula would do the same job as the VLOOKUP in the previous example: =INDEX(G:G,20,1).

      12. MATCH

      The MATCH function allows you to find the position of a value within a range of cells. Oftentimes, Excel users deploy a combination of INDEX and MATCH instead of VLOOKUP due to its limitation (e.g. VLOOKUP can’t extract values to the left of the lookup field). In the previous example, you had to specify the row belonging to the order number. But if you didn’t know it, you could use the MATCH function within the INDEX function. The MATCH function would look like this: =MATCH(10318,C:C,0). Placed within an INDEX function, it can replace the argument where in the previous example, we set a value of 20: =INDEX(G:G,MATCH(10318,C:C,0),1). By doing this, you have a more flexible version of the VLOOKUP function. You can also create dynamic formulas using INDEX and MATCH that use lookups for both the column and row.

      13. COUNTIF

      The COUNTIF function allows you to count the number of cells in a range that meet a specified condition. Let’s count the number of values in the data set that are Motorcycles. To do this, you would enter the following formula: =COUNTIF(M:M,”Motorcycles”).

      14. COUNTA

      The COUNTA function is similar to the previous function, except it only counts the number of non-empty cells. With no criteria, it is helpful to just the total number of values within a range. To calculate how many cells are in this data set, you can use the following formula: =COUNTA(C:C). If there are no gaps in data, then the result should be the same regardless of which column is used. And when combined with the UNIQUE function, you can have an easy way to count the number of unique values.

      15. UNIQUE

      The UNIQUE function returns a list of unique values within a range, and it’s a much easier method than the old-school way of extracting unique values. If you wanted to extract all the unique product lines in column M, you would enter the following formula: =UNIQUE(M:M). If, however, you just wanted to count the number of unique values, you could embed it within the COUNTA function as follows: =COUNTA(UNIQUE(M:M)). You can adjust your range if you don’t want to include the header.

      This is just a sample of some of the useful Excel functions that accountants can utilize. If you are familiar with them, you’ll put yourself in a great position to improve the efficiency of your workflow and make your spreadsheets easier to use. Plus, you can confidently say that you are highly competent with Excel, which can make your resume more attractive and make you better suited for accounting jobs that require advanced Excel skills — and there are many of them that do!.

      If you liked this post on 15 Excel Functions Accountants Should Know, please give this site a like on Facebook and also be sure to check out some of the many templates that we have available for download. You can also follow me on Twitter and YouTube. Also, please consider buying me a coffee if you find my website helpful and would like to support it.

      H2Etaxes1

      How to Calculate Taxes in Excel

      by with No Comment accountingbudgetspersonal financetemplate

      Want to estimate how much you might owe in taxes next year? If you are self-employed or have other income besides what you get from an employer, then you may find it useful to plan ahead of time and determine how much you might owe to ensure that you are putting aside enough money for taxes. It’s not a fun process but it can save some headaches later on. The good news is that Excel can make that process easy. Below, I’ll show you how you can calculate and estimate your taxes in Excel. And if you’d just prefer to download the file that I have created, scroll to the bottom of this page.

      Determining your marginal tax rate

      To estimate your taxable income and marginal tax rate, the first thing you’ll need is a table for the tax brackets. For this, I will use the schedule for federal income tax brackets 2021 found here.

      I can’t simply copy the table into Excel as I will need to format it a little differently (the values contain text and won’t be helpful if I need to do a lookup). The table needs to be organized by income threshold rather than tax rate. This is how I have set it up in Excel:

      Income tax brackets set up in Excel.

      To make this table easier to reference to, I am going to create named ranges for these tax brackets plus the income I am going to enter in. This will make it easier to follow along.

      If I want to look up the incremental tax bracket for a given level of income, I can accomplish this using a VLOOKUP formula. This is the formula I would use to accomplish that:

      =VLOOKUP(Income,TaxBrackets,2)

      What it is doing is taking the income number, and looking up the tax bracket table, and pulling in the second column (the tax rate). The VLOOKUP formula doesn’t look for an exact match (as I have left the last argument empty) and it will pull the closest number without going over. This is where it’s important to put in the numbers that the tax bracket start at, rather than a range. Using this formula, it correctly tells me that income of $100,000 would be at the 24% tax bracket as it does not yet reach the minimum amount for the next bracket — $164,926:

      Determining the marginal tax rate in Excel.

      That tells me the correct tax bracket but I still need to calculate the taxes that are due at each level, which I will cover in the next section.

      Determine how much you owe at each tax bracket

      For the first tax bracket, I will need to determine if the income level reaches the second tax bracket. If it does and the income is at least $9,951, then I can multiply that by the tax rate of 10% as that would be the maximum that can be taxed at the first bracket — 9,951 x 10%. If the income is not at least $9,951, then I just multiply the total income by the tax rate. Here is what the formula looks like using named ranges:

      =IF(Income>=IncomeLevel2,IncomeLevel2-IncomeLevel1,Income)*TaxRate1

      For the second tax bracket calculation, I can follow similar logic. I will multiply the difference between the start of the third and second income levels. Here’s how that calculation looks:

      =IF(Income>=IncomeLevel3,IncomeLevel3-IncomeLevel2,MAX(0,Income-IncomeLevel2))*TaxRate2

      I also use the MAX function just in case there is a negative number (where the income doesn’t even reach the next level). The same logic can now be applied for all of the remaining tax brackets except for the last one. Like the first one, it needs to be calculated differently. In that case, I just need to know if the income is above that threshold. And if it is, I take the difference between it and the total income, and multiply it by the highest rate:

      =IF(Income>=IncomeLevel7,Income-IncomeLevel7,0)*TaxRate7

      If the income isn’t above the last level, then I put a 0 and multiply that by the tax rate. Now, when I’m all finished, I can sum up the tax owing at each level and come to a total tax number that would be due based on a given income number:

      Tax owing calculation in Excel.

      At this stage, you could now decide to deduct how much you may have already paid in taxes and any deductions or credits that you are entitled to.

      But I’m not going to go any deeper here because there are too many different variations from one country and jurisdiction to the next when it comes to taxes. However, this should at least give you a good starting point for doing the rest of your estimation, however detailed you want it to be. But by at least estimating the taxes owing and deducting how much you have already paid, you should have a good idea of how much you might owe come tax time, under a worst-case scenario.

      If you’d like to just download the file that I created when making this post, you can do so here.

      If you liked this post on How to Calculate Taxes in Excel, please give this site a like on Facebook and also be sure to check out some of the many templates that we have available for download. You can also follow us on Twitter and YouTube.

      H2Etax

      How to Calculate Tax Included in an Invoice

      by with No Comment accountingaccounts receivablebeginnerinvoice

      If you are creating an invoice and need to account for taxes, usually you just need to multiply the subtotal by the percentage due for taxes. However, it gets trickier when the tax amount is already included within the invoice total and you need to work out what the amount relating to tax is. This is important if you need to determine how much in taxes you need to claim on an expense or how much you need to collect if you’re the seller. Below, I’ll go over a sample invoice calculation to show how can determine the tax amount whether it is included in the total or not.

      Calculating taxes on an invoice

      Let’s start with the basic calculation. This is how you might normally determine the taxes on an invoice and the total invoice value:

      Sample invoice calculation including taxes.

      The calculation is straightforward as what you do is just take the subtotal, multiply that by the tax rate, and add that back to the subtotal. Another way is to just take the subtotal and multiply it by a factor of 1 + the tax rate. In this case, it would $100 x 1.10. But let’s pretend we don’t know the subtotal and just know that the invoice total is $110.00 and the tax rate is 10%. In order to calculate the pre-tax amount, we need to do the steps in the opposite order. To prove this out, let’s use a bit of algebra:

      $100 + ($100 x 10%) = $110

      This can be simplified as follows:

      $100 (1 + 10%) = $110

      Now let’s solve for $100 which I will assign a variable of ‘y’ to:

      y (1 + 10%) = $110

      To solve for y, all we need to do is move the factor of 1 + the tax rate and divide $110 by that:

      y = $110/(1 + 10%)

      Taking $110 and dividing by 1.1 will give us a value of $100. And so what our end result comes out to is essentially this:

      invoice total / (1 + tax rate) = pre-tax amount

      To calculate the tax, all that’s needed then is to take the total and subtract the pre-tax amount.

      Now that the logic is set up, let’s convert this into an Excel formula:

      Invoice calculation when the tax amount is included.

      Similar to how multiplying by a factor of the pre-tax amount by 1.1 (when the tax rate is 10%) would get you to the invoice total, dividing the total by 1.1 would get you to the amount before taxes. If the tax rate were 5%, then you would use 1.05, etc.

      If you liked this post on How to Calculate the Tax Amount When it Is Included in the Total, please give this site a like on Facebook and also be sure to check out some of the many templates that we have available for download. You can also follow us on Twitter and YouTube.

      amort

      2 Excel Functions That Can Eliminate the Need for an Amortization Table

      by with No Comment accountingfunctionsintermediatetips & tricks

      An amortization table is a useful tool when you need to calculate interest payments, principal payments, and to track the balance that’s owed on a loan. However, you don’t have to create a full schedule to get these values and below I’ll show you two functions that can get you that information quickly and easily. First, let’s start with what a typical amortization schedule looks like.

      Creating the amortization schedule

      When you set up an amortization schedule, you’ll track the balances, interest, and principal payments. It often looks something like this:

      Amortization table in excel.

      You could use the table to determine what the balance is at the end of period 10 or to add up all the interest payments up until that point. However, there’s another way to arrive at those totals, and that’s using two functions that are available in the newest version of Excel: CUMIPMT and CUMPRINC.

      Using the functions

      In the amortization schedule, we can see that the ending balance of the $100,000 loan by the end of period 10 is $85,016.67. We can use the CUMPRINC function get to that total as well. The function takes on the following arguments:

      Cumprinc arguments.

      To calculate the cumulative principal payments, I’ll enter the formula with the following arguments:

      =CUMPRINC(0.05/12,60,100000,1,10,0)

      This gives me a total of -$14,983.36. When added to $100,000, it nets out to a balance of $85,016.64 — within just a few cents of the amount on the amortization table. The function gives you the flexibility to specify which periods you want to extract and so you aren’t limited in just tabulating the totals for the first 10 periods or starting from the beginning. You can start from period 13, or the second year, and so on.

      If you want to calculate the total interest payments, then that’s where you can use the CUMIPMT function. It has the same arguments as the CUMPRINC calculation, so the formula will look very similar to what’s above:

      =CUMIPMT(0.05/12,60,100000,1,10,0)

      This tells me that the cumulative interest payments during the first 10 payment periods is $3,887.87. This matches what I would get by adding the interest payments in my amortization table over the same period, this time to the penny.

      Should you use these functions instead of an amortization table?

      On older versions of Excel, you won’t have access to these functions but if you’re using Microsoft 365 or Excel 2019, then these functions are available and can potentially serve as replacements for an amortization table. Now, if you need the table for audit purposes it may not be possible for you to do without an amortization table completely. But if you’re only generating the table just to determine how much you’ve spent on interest or what your balance will be at some point in the future, then these functions can certainly replace doing a full-blown amortization table.

      If you liked this post on 2 Excel functions that can eliminate the need for an amortization table, please give this site a like on Facebook and also be sure to check out some of the many templates that we have available for download. You can also follow us on Twitter and YouTube.